Limits of gnoseology

Dedicated to Beyon Miloyan

---

1. Regardless of the exact epistemological conclusions a scholar might end up making, it is clear that they should all stem from the same root that all theories of knowledge share. That is, the duality of the subject and object of knowledge which is fundamental to the very act of cognition (knowing).

2. The duality of the subject and the object of knowledge is the primal duality that epistemology is about in its essence. It is the punctum pruriens, the itchy spot that irks the contemplative mind and propels philosophical thought ever forward. This duality, intrinsic to the act of knowing, sparks the Aristotelian wonder, which is in turn what creates philosophy and gives it life^[1]. Therefore, it is clear that the actual goal of epistemology is to soothe that itch. To strip the cloak of wonder from knowledge; to find such springs for philosophical inquiry that would allow it to pursue the path of knowledge without being hindered by the subject of knowledge seemingly starting to double.

To dissolve this factual duality means to integrate both its parts into a single entity. The theory of knowledge is and must be monistic, and all attempts to formulate such a theory generally concur on this. The only difference is that some wave the monistic flag openly, whereas others try to accomplish monism under the guise of less radical premises.

3. Generally speaking, there are two main schools of thought that one might follow in the pursuit of this aim. This number, two, is determined by the number of beginnings for a new thought the very act of knowing contains. We should only consider a third approach if the first two prove insufficient. This alternative path demands a transformation of reality, which means it cannot be considered purely theoretical.

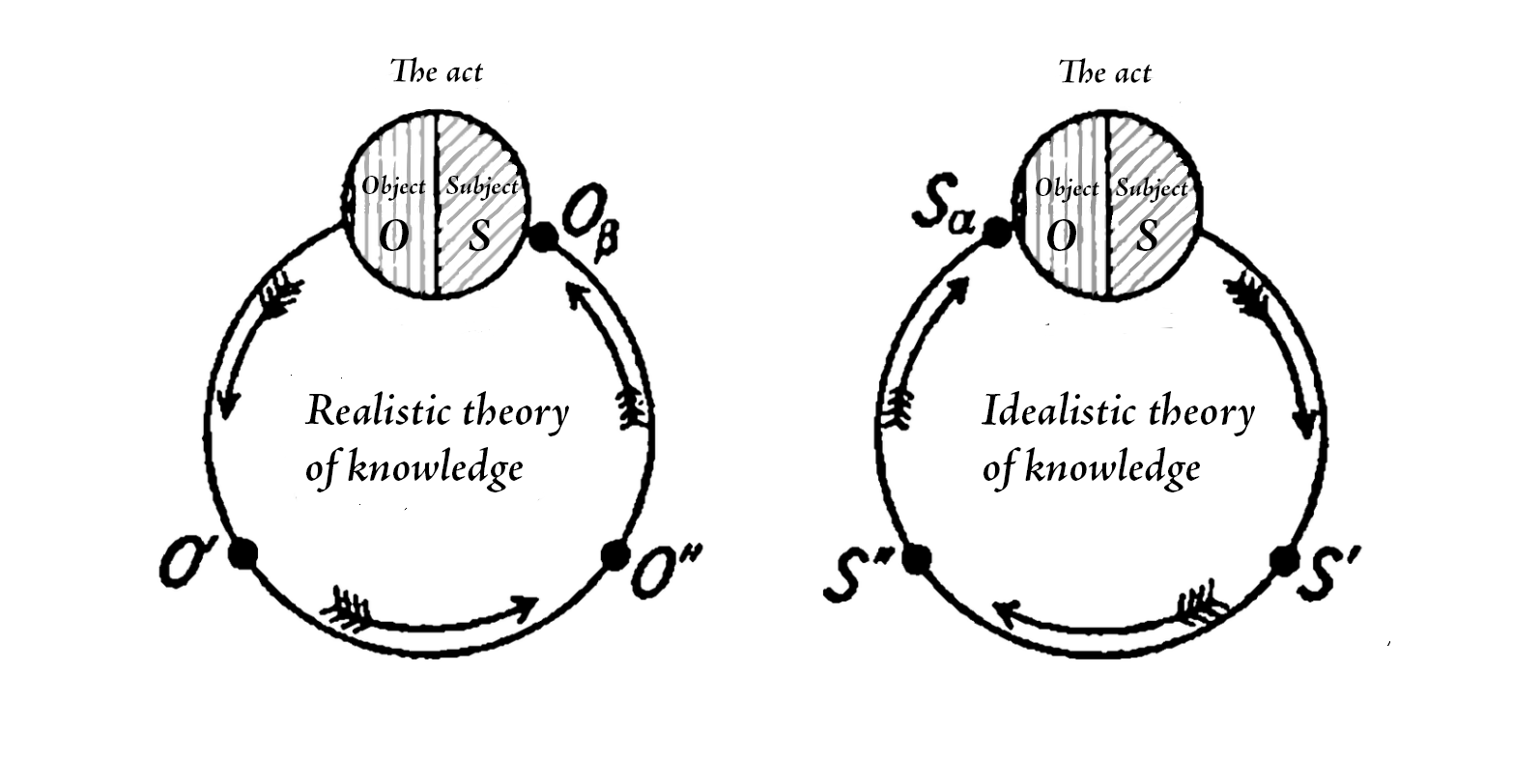
4. The first epistemological path takes its root in the objective moment of knowledge, presuming the object $O$ to be immediately known. By means of a series of transformations on and suspensions of $O$ ($O\mathit{\text{'}}$, $O\text{'}\text{'}$, etc.), epistemology follows the path of $OO\text{'}O\text{'}\text{'}{O}_{\beta }$, bestowing more and more attributes upon $O$ along the way. When the set of those attributes $\beta$ becomes complex enough, then the epistemology of this kind will equate $O_{\beta }$ to some other moment of the act of knowing, a subject of $S$, and therefore destroys $S$ as a primary reality. Even though $O$ and $S$ were initially equal, they lose this status. $O$ becomes something primary, something epistemology believes, and $S$ is derivative, something epistemology knows. To summarise, there is, in essence, only $O$ and its derivatives: $O\text{'}, O\text{'}\text{'}, ..., O_{\beta }=S$. And as such, the subject is deduced from the object, and the job of epistemology can henceforth be considered done. This kind of theory of knowledge, depending on the exact character of the path and the purity of the end results, has different names: sensualism, positivism, phenomenalism, realism, empirical criticism or immanentism. Yet the most notable and consistent realisation of this approach in the history of philosophy would be intuitivism or mystical empiricism, developed by Lossky.

The second epistemological path is the opposite of the first. It starts with the subjective moment of knowing, $S$, and by means of transforming this $S$ into $S\text{'}$, $S\text{'}\text{'}$ and, finally, $S_{\alpha }$, by giving it a set of attributes $\alpha$, eventually arrives at such an $S$ that can be equated with the object $O$. As such, the object is deduced from the subject, and on this deduction, again, the job of epistemology here can be considered done. This type of theory of knowledge, again, has many forms. Depending on the nature of the path and the purity of the results, it can be known as idealism, rationalism, panlogism, etc. One of its most refined forms, second only to Hegel's, is the system of panmethodism developed by Herman Cohen and his closest disciples.

5. Different forms of realism and rationalism represent two parallel lines that define the scope of epistemology. This epistemology aims to remain within human reality and refuses to consider alternate worlds or novel experiences. Being unable to either choose a path (for epistemology is substantially rooted in believing in either not-I or I) or devise a new one, epistemology inevitably finds itself confined by those limits that were devised for it by its faith in reality, or rather lack of faith in higher powers. Epistemology lends itself equally well to objective and subjective teachings. That is its central antinomy, and resolving this antinomy requires stepping outside the realm of humanism. Yet to demonstrate this antinomy to you more clearly, I will briefly outline the core essence of both epistemological paradigms. Our goal is not to present a historically accurate account of each school of thought but rather to capture the spirit of their teachings. Without restricting ourselves to specific names and books, we will explore the ideas associated with rationalism and realism, aiming to demonstrate and see for ourselves that each of these paradigms can be valid as long as we embrace its foundational assumptions.

So how does each epistemological paradigm answer the central question of knowledge?

I. Rationalism

6. What is knowledge? To answer this fundamental question^[2], we must highlight an aspect of knowledge that pertains to all forms of cognitive activity. We need to describe knowledge in general, knowledge itself. In other words, we need to articulate what we know about knowledge.

What do we know about knowledge? First, we know that knowledge is not ignorance. We know that knowledge does not equal ignorance. When I know, I am not in a state of not knowing; and I know that I do not not know. Knowledge knows about itself, that is, it knows that it is indeed knowledge and not something else. That is, it identifies itself primarily by contrasting itself with ignorance. To contrast ignorance with knowledge is the only way to know what knowledge is. These arguments might seem too vague and self-evident. Yet they contain, in brief, everything I shall discuss below.

7. Differentiation is the necessary and sufficient condition for knowledge. I say: necessary. That means that without differentiation, there is no knowledge; differentiation is necessary for knowledge. If we do not differentiate between knowledge and ignorance, then we do not know knowledge. I also say: sufficient. That means that once you have differentiation, you do not need anything else to attain knowledge. If there is differentiation, then there is knowledge, eo ipso. Differentiating between knowledge and ignorance is the knowledge of knowledge, for if we differentiate between the two, then we know, even if only vaguely, what the difference between them is; we know the nature of knowledge.

8. Perhaps you might argue that this is only true in the context of knowledge of knowledge, not knowledge in general. Yes, in this case we are differentiating between knowledge and ignorance. That is, we are differentiating between the object of knowledge (that is, knowledge itself) and something that is not the object of knowledge (that is, ignorance). It follows that we have already cognised the nature of knowledge itself, regardless of this or that object of knowledge, in contrast with everything that is not knowledge, or rather, everything that makes the knowledge (no matter of what) knowledge. This is differentiation, and the question 'what is differentiated from what?' is answered not by the nature of knowledge, but by this particular application of the act of knowing. And, if differentiation was not the nature of knowledge in general, it could not be it in this particular case either, when the object of knowledge is knowledge itself, because in defining this attribute of knowledge as an act, we said nothing of the specific nature of its object (in this case, knowledge itself). Even though we said 'knowledge of knowledge', the second instance of 'knowledge' remains a purely formal symbol of objects in general [we are using the mathematical method of undetermined coefficients, or Descartes's method, as well as Bugaev's method of discontinuous functions].

9. What does this mean? It means that knowledge fundamentally involves differentiating between the object we intend to know and everything else. To know is to distinguish the object of knowledge from what we have yet to understand, setting it apart from everything that is not knowledge. To know means to differentiate and distinguish. The nature of knowledge is in distinction, differentiating and distinguishing.

10. This is on the one hand, as we got sidetracked from the object of knowledge. However, on the other hand, we could consider the object of knowledge as well. Then it becomes clear that there is some kind of difference between knowledge that differentiates an object and knowledge that differentiates the knowledge of objects from ignorance. The former focuses on knowing objects, and the latter focuses on differentiating between the knowledge of objects and the ignorance of objects. The former is just knowledge ($A_1$); the other is the knowledge of knowledge, so to speak, the second degree of knowledge ($A_2$). In the former case, knowledge is consumed by its objects; it does not remember itself. In the latter case, it knows objects but at the same time observes itself and what constitutes its activities. Therefore, in the latter case, the object of knowledge for ($A_2$) is knowledge itself ($A_1$), which was previously the knower, the knowing subject.

11. But knowledge $A_2$ that is directed upon itself ($A_1$) and has itself as its object can be differentiated from the ignorance of itself, that is, knowledge that is not directed upon itself. Therefore, there is an act of differentiation by means of which knowledge ($A_2$) is contrasted against the ignorance of knowledge. In other words, there is knowledge that has the knowledge of knowledge ($A_2$) as its object; that is, there is knowledge of the third degree ($A_3$).

12. We can go further. We can differentiate between the third power of knowledge $A_3$ and the third power of ignorance. This process of differentiation would represent the fourth power of knowledge ($A_4$), and so on, ad indefinitum. I say ad indefinitum, that is, for an indefinitely long time. That means that as we ascend this ladder of knowledge:

$A_1, A_{2,} A_3, A_4, A_{5, }... A_n, A_{n+1}, A_{n+2}, ... \left(1\right)$

we do not face any obstacles that would break this series. This uninterrupted ascent is a direct result of the iterative or repetitive nature of the differentiating act of knowing. While the object of knowing changes with each iteration, the act itself remains consistent, making it always formally satisfiable at the outset of the series. Since we know it is satisfied here, it follows that it is satisfiable everywhere.

13. On every new step of the ladder (1) (that we can refer to as $\left\{A_i\right\}$), we are repeating the same act. That is, 'what was differentiated by the previous degree will have been differentiated on the degree that follows; the cognitive process of the former will be known on the latter; what was previously the subject becomes the object'^[3]. Every act of the series (1) is the reflection of knowledge upon itself. Re‑flexio means re-turn. The prefix -re suggests a double movement, towards something and all the way back. To reflect upon oneself means: 1) to return to oneself, 2) to look at oneself closely, 3) to recognise, or rather, to come to know oneself.

14. Our words knowledge, cognition, conscience, self-actualisation, self-awareness are, in essence, terms for reflective acts of knowledge of this kind.^[a] Some of the words listed are not part of the series $\left\{A_i\right\}$ and represent, so to speak, intermediary terms. This will become clear later.

15. Any criticism is, in its essence, a self-reflection of the same kind. The first criticism ($K_1$) examines the work ($P$). The second criticism ($K$), or an anti-criticism, a criticism of a criticism, is $K_2$. The third criticism, or a re-criticism ($K_3$), is a criticism of a criticism of a criticism, a criticism of an anti-criticism, and so on. We have a series that starts with $P$:

$P, K_1,K_2,K_3,K_4 K_n,K_{n+1},K_{n+2}, \left(2\right)$

Every one of those criticisms is a degree above the preceding. The substitution of a criticism of the nth power ($K_{\mathrm{n}}$) with a criticism of a (n+1)th power ($K_{n+1}$) is what constitutes the history of any branch of science. Any process of knowing is, in essence, this path from criticism $K_n$ to a criticism of that criticism, that is, $K_{n+1}$.

17. Knowledge consists of an infinite series of reflective, self-oriented acts that synthetise and synergise to form a single entity. The group

$\left\{A_i\right\} i = 1, 2, 3, ... n ...$

is not just a set of separate acts $A_i$, but also their unity that can be conceptualised as a single entity. This thought is not a groundbreaking novelty. It permeates the entire history of philosophy, the ancients and the moderns alike. Fichte speaks of it in his Wissenschaftslehre. Yet it was systematically articulated for the first time by Schelling in his System of transcendental idealism. Here, Schelling set out to present the history of knowledge as a series of reflective acts:

$A_1, A_2, A_3, A_4, ... A_n, A_{n+1} ... (1\text{'}),$

that he refers to as the potencies or powers (Potenz) of knowledge. He uses the mathematical notation for exponents:

$A^1, A^2, A^3, A^4, ... A^n, A^{n+1} ... \left(2\right).$

18. I will take the liberty to somewhat clarify and improve on Schelling's notation. We have an object of knowledge, an entity of a kind that will henceforth consider singular, united, unbreakable and impossible to simplify. It is appropriate to use the symbol 1 to represent this entity, as this symbol naturally aligns with the concept of an object. Our understanding of the knowable object arises from distinguishing it from everything else and perceiving it as a unified, indelible entity, as one. However, there is a deeper meaning to this symbolism that we shall explore later. It is important to remember that, in epistemology, the object 1 is defined by the act of differentiation.

19. To this object, the 1, we apply the act of differentiation $A$. The symbol $A$, therefore, stands for the act of differentiating a particular matter from what is not itself. As such, we denote the knowledge of the first degree, $A_1$, with the following formula:

$A_1=A\left(1\right) \left(3\right)$

or, if simplified,

$A_1=A^1 (3\text{'})$

However, as knowledge is the knowledge of what?, it does not matter whether we explicitly use the word object or not. The act of knowing inherently includes understanding an object, just as the concept of an object involves the act of knowing that distinguishes it. To express this idea in symbolic terms, we can say that since multiplying by one does not alter the original number, we can omit the one. Thus, we can formulate the operation of knowledge as follows:

$A_1=A=A^1 \left(4\right)$

The differentiation of this differentiation $A^1$, that is, $A_2$, we have to represent as follows:

$A_2=A\left(A_1\right)=A\left(A^1\right)=A\left(A\right) \left(5\right)$

And the differentiation of this differentiation, $A_3$, via

$A_3=A\left(A_2\right)=A\left[A\right(A^1\left)\right]=A\left[A\right(A\left)\right] \left(6\right)$

Then the differentiation of this differentiation:

$A_4=A\left(A_3\right)=A\left[A\right(A_2\left)\right]=A\left\{A\right[A\left(A\right)\left]\right\}=A\left\{A\right[A\left(A^1\right)\left]\right\}=A\left\{A\right[A\left(A\right)\left]\right\} \left(7\right)$

etc. And generally:

$A_{n+1}=A\left(A_n\right)=A\left[A\right(A_{n-1}\left)\right]=A\left\{A\right[A\left(A_{n-2}\right)\left]\right\}=\frac{A\left\{A\right[A...\left]\right\}}{n times} \left(8\right).$

From here, it is natural to present these expressions of iterative operations as symbolic degrees of the operator $A$. We should note that in each of $A_i$, the operator $A$ is repeated $i$ times, and we therefore replace the indices of all $A_i$ with the respective exponents in such a way that:

$A_i=A^i \left(9\right) (i=1,2,3,4,... n, ...)$

or, if expanded,

$A_1=A^1, A_2=A^2, A_3=A^3, A_4=A^4, ..., A_n=A^n, A_{n+1}=A^{n+1} \left(10\right).$

As such, we get the series of 'potencies of knowledge', or, to be more precise, potencies of knowledge in a new form. The series (1) is replaced by this new series:

$A^1, A^2, A^3, A^4, A^5, A^6, ... A^n, A^{n+1}, A^{n+2}, A^{n+m} ... \left(11\right).$

But before we proceed with our argument, let us clarify a small point. You are perhaps confused as to what grounds we have to replace the unknown operation on 1 in formula (3) with a symbolic multiplication of formula (3'). First, I shall note that our formulas are symbolic and hypothetical. Yet we must show that, indeed, our symbols can be used in multiplication. Indeed:

First, $A\left(1\right)$ must be such that it is equal to $A$, for the act of knowing $A$ is ipso facto the act of knowing 1. It follows that no matter whether we choose a special symbol to denote that, the meaning will be the same. Therefore,

$A\equiv A\left(1\right) \left(12\right)\left(I\right),$

where ≡ is the identical to sign. Second, the relation of $A_1$ to 1 must be the same as the relation of $A_2$ to $A_1$, $A_3$ to $A_2$ and so on, for the two contiguous potencies $A_n$ and $A_{n-1}$ are only differentiated by the act of knowing. You will ask: why relation and not difference? Because different potencies are distinct entities, they cannot be summed with or deducted from each other ('five chairs minus three pots of ink' or 'five souls without three benches'). It follows that to compare them, we ought to look at their relation. Therefore:

$=\frac{A_n}{A_{n-1}}=\frac{A_{n-1}}{A_{n-2}}= =\frac{A_2}{A_1}=\frac{A_1}{1} \left(13\right)\left(II\right).$

Formula (12) shows that the symbolic operation with $A$ cannot be equated with the contiguous $[A\ne A+1]$. Formula (13) proves that this operation cannot be potentiation, raising to an exponent, because:

$[...\ne \frac{{A^A}^A}{A^A}\ne \frac{A^A}{A}\ne \frac{A}{1}]$

There is only one operation left, which is multiplication. We could, of course, provide a strict mathematical proof using the finite difference method and solve a functional equation. But I will save this for future research, especially since it would seem rather unsuitable for this popular presentation.^[4]

20. One way or another, we now have the series (11). We are now facing the question: what to use to denote the yet unknown object of knowing, our 1? In other words, what is it from the point of view of the knower, of the knowing subject? After all, we still speak of the unknown, so we must therefore know it at least in some way, for it is impossible to speak of something that is completely unknown. Otherwise, our words would be entirely empty and meaningless. Now, what is this object '1' from the point of view of the iterative operator $A$? How do we bring symmetry into our symbolic notation? How do we make our symbols homogeneous? If we speak formally, we can say: we have not yet applied any acts of differentiation to our object of differentiation, to the '1', i.e. $i=0$. In this sense, it can be denoted, from the point of view of the process of knowing, as $A_0$ or, to use the newly designated, transformed symbols, as $A^0$. Indeed, this designation appears quite fitting:

$1=A_0 \left(16\right)$

But $A_0=A^0 \left(17\right)$

And $A^0=1$

for any number raised to the power of zero equals one.

As such, if we denote the unknown object with $A^0$, we will not diverge from the notation we chose initially but rather improve upon it. Previously, we would denote the object of knowledge with 1, as something that was distinct from $A$. Now, as $A^0$, this '1' is formally homogeneous with the entire series (1) or (11) and is therefore part of the iterative series. In other words, the object of knowledge is now part of the series of potencies of knowledge.

It might make sense to say a few words about the zero potency of knowledge, that is, about the thing. The conclusion that $A^0$, the knowledge of the zero potency, is an object or a thing, '1', a unit of cognitive activity, should not surprise us or seem unexpected. Indeed, from the gnoseological point of view, the very fact that we speak of a thing proves that the thing is knowledge of some kind. Otherwise, we would speak and not know what we are saying. Every single thing is knowledge of some kind. What kind, though? As knowledge, it should be posited by the spirit, but in such a way that the spirit would not know it is positing the thing, so that it would appear to the spirit as the final result, even though it is an act of the spirit.

21. We are now facing the question: how can we understand this yet unknown object $A^0$ that is to be known?

There is more: how is it related to the process of knowing? We shall first recall what each $A^n$ is. It is the knowledge of the preceding knowledge, $A^{n-1}$:

$A^n=A\left(A^{n-1}\right) \left(18\right)$

that is, $A^n$ is the act of differentiation $A$, applied to $A^{n-1}$.

Then $A^1$ is the knowledge $A^0$; and $A^0$ is an object, a 'thing'. Yet all knowledge is an object for the degree of knowledge that follows. Every $A^{\mathrm{n}}$ is an object for $A^{n+1}$, but what is it on its own? If we use the terminology we devised, we ought to say: $A^0$ (i.e. 1) is also knowledge. But in that case, what is $A^1$ the knowledge of? There is the knowing kind of knowledge; there is the reflecting knowledge; there is the self-reflecting knowledge, and so on. But $A^0$ is not relevant here. Even though it is knowledge, it is not yet known as such, as knowledge. $A^0$ is the unconscious knowledge; the knowledge without knowing. This is knowledge that has not reached the full state of knowledge, that has not yet attained consciousness, that has not yet been known. As such, the object of knowledge itself is a special kind of knowledge, the unconscious kind. To reiterate, we will say: the object of knowledge is also knowledge, but unconscious knowledge. From the point of view of knowledge, what is being known is unconscious knowledge, and therefore the process of knowing is nothing other than the realisation of what is already within the spirit but in the unconscious form.

22. Let us continue. You know, of course, that in algebra, there are negative powers with negative exponents. To build upon our symbols further, we can think about what these might mean:

$A^{-1}, A^{-2}, A^{-3}, A^{-4}, , A^{-n}, A^{-n-1}, \left(19\right)$

or, which is the same thing, the symbols:

$\frac{1}{A},\frac{1}{A^1}, \frac{1}{A^2}, \frac{1}{A^3}, , \frac{1}{A^n}, \frac{1}{A^{n+1}} \left(20\right)$

To answer this question, let us try to cognise one of such postulated yet currently unknown to us potencies. For example, let us look at $A^{-3}$. To cognise it means to apply the act of differentiation $A$ to it. We get:

$A\left(A^{-3}\right)=A^{-2} \left(21\right)$

Again, that is still not quite clear. Let us cognise $A^{-2}$.

We get:

$A\left(A^{-2}\right)=A^{-1} \left(22\right)$

By cognising $A^{-1}$, we find:

$A\left(A^{-1}\right)=A^0=1 \left(23\right)$

Therefore, by applying the act of differentiation $A$ to $A^{-3}$ three times, we arrive at the subconscious knowledge, or the object 1. It is clear that by cognising $A^{-3}$ even more times, we would get $A^1$, $A^2$ and so on. We could get these results immediately by applying the manifold act of differentiation:

$A^3\left(A^{-3}\right)=A^0=1 \left(24\right)$ $A^4\left(A^{-3}\right)=A^1 \left(25\right),$

or, if we consider the symbol of negative potency as one divided by the same potency but positive, we get:

$A^3\left(\frac{1}{A^3}\right)=1 \left(26\right)$ $A^4\left(\frac{1}{A^3}\right)=A^1 \left(27\right)$

23. In other words, negative potencies are such potencies that need to have the differentiation process $A$ applied to them several times in order to arrive at a degree of consciousness of some kind. Or: negative potencies are the unconscious, or, to put it even better, subconscious layers of the spirit that go deeper and deeper into objectivity. These things are more thinglike than actual things, quam res reales. It is clear from here that the deeper such res realior lies in the spirit, the more intensive the differentiation activities of knowing need to be to recognise the res realior.

Perhaps you are wondering: what exactly are those negative potencies of knowledge? And then we wonder: is it possible to explicitly, matter-of-factly cognise those deeper levels of thinghood? Are we not bound to always remain by the abstract, gnoseological knowledge of them, for a concrete knowledge of them would raise them up to the degrees of consciousness and therefore strip them of the only attribute that makes us want to cognise them concretely? Should we not think that this exact attribute (i.e. a higher level of subconsciousness rather than thinghood, a thinghood that is more thinglike than the actual things) would be lost as a result of this process? We should answer the latter questions before we address the first.

Indeed, by means of gradual differentiation, we would strip these lowest potencies of their intrinsic thinghood. And such is, necessarily, the scientific knowing, which methodically goes through every degree and thereby acquires the ability to draw connections between objects of knowledge, all the while still clothing reality in the translucent garment of concepts. Yet there can also be the non-methodical knowledge, the kind of knowledge that immediately takes the object through several potencies and introduces the subconscious in the field of knowledge (which is Hartmann's definition of mysticism). Therefore, there is also the knowledge of those subconscious acts per se.

24. Yet there is one more way to approach negative potencies. We have previously considered the symbol $A$ not only as an operator, but also as an operandum. Not only as a symbol one operates with, but also as a symbol one operates upon. We have examined the symbols of negative potencies as knowable entities, as operandums. From here, we can similarly examine them as operators, as entities that cognise, but entities of a very special nature. What kind of nature? To answer this question, let us apply our operator to one of the positive potencies we already know and see what happens. Let us consider $A^2$ and take $A^{-1}$ as an operator:

$A^{-1}\left(A^2\right)=A^1 \left(28\right)$

or:

$A^{-1}\left(A^2\right)=\frac{1}{A}\left(A^2\right)=A^1 \left(29\right)$

25. As such, applying the operator $A^{-1}$ to a positive potency lowers its degree, its rank. In other words, the operation $A^{-1}$ is directly antagonistic to the operation $A$. $A$ is an act of differentiation; $A^{-1}$ is an act of integration. $A$ is an act of distinction; $A^{-1}$ is an act of transfusion and confusion. $A$ is an act of knowledge; $A^{-1}$ is an act of ignorance, a reversal of knowledge. $A$ is an act of forming an utterance; $A^{-1}$ is the act of destroying an utterance. $A$ is the gnoseological multiplication; $A^{-1}[=\frac{1}{A}]$ is the gnoseological division. $A$ is an act that raises the rank of a potency of knowledge; $A^{-1}$ is an act that lowers this rank. $A$ is an act of reflection; $A^{-1}$ is an act of inflection, of returning knowledge into itself, yet not unto itself. Not in, but an ѕісһ. To summarise, $A$ and $A^{-1}$ are antagonistic and conflicting, they are polar opposites.

26. As such, we arrive at a novel conception of knowledge, with the word knowledge being understood not only in the sense $A$, but as the entire scope of knowing activities of the spirit.

Knowledge, on the whole, is composed of a series of acts of reflection that is infinite in both directions; that is if we use the word 'reflection' in a broad sense to include the concept of inflection, specifically from the series:

$... A^{-n-1}, A^{-n}, ..., A^{-3}, A^{-2}, A^{-1}, A^0, A^1, A^2, A^3, ... A^n, A^{n+1}, ... \left(30\right)$

This series, taken as a transfinite group, defines two elements, $A^{\omega }$ on the right and $A^{-\omega }$ on the left, that serve as the bounds of the series and therefore do not belong to it themselves. Applying the operation $A$ to any element of the series moves knowledge towards $A^{\omega }$, whereas applying the operation $A^{-1}$ pushes it towards $A^{-\omega }$. Series (30), since it defines the out-of-bounds element $A^{\omega }$, i.e., as we are considering it as an ascending series, is called philosophy, φιλοσοφία, the knowledge-love. But we can consider the same series (26) as defining the out-of-bounds element $A^{-\omega }$, i.e. consider it as a descending series. In this case it would be appropriate to refer to our series (30) with the neologism nikosophia, νεικοσοφία‚ the knowledge-enmity. However, that would be, of course, not meant as derogatory, but only used to point to the departure from reflection, attachment to the roots of existence and the murky darkness of the primordial night. $A$ is the act of philosophising, and $A^{-1}$ is the act of nikosophising.

27. Every element of the series is what is being cognised, in relation to the preceding element, and the cognising subject, in relation to the following element. Operator $A$ makes the knowable into the cognising, and operator $A^{-1}$, on the contrary, makes the knower into what is being known. Therefore $A$ is the act of going from objectivity to subjectivity, from the object to the subject, from knowledge to more knowledge. $A$ is the operator of subjectivation. On the contrary, $A^{-1}$ is an act of going from subjectivity to objectivity, from the subject to the object, from more knowledge to less knoweldge. $A^{-1}$ is the operator of objectivation.

28. And such, every act of reflection is the subject and the object joined together; the subject is showing its left side, and the object its right side. Each element of the series, a potency, is a subject and object. But an object is what we refer to as the real beginning, and the subject is the ideal beginning. Therefore, every act of knowledge is real in relation to the act that follows it, and ideal relative to the act that precedes it. Every act of knowledge is ideal and real, i.e., ideal-real or real-ideal.

29. It follows that in every potency of knowledge the ideal and the real, the subject and the object are not entirely disparate, even though they do not merge and interfuse. They form a balanced duality, and objects of knowledge are given immanently to the process of knowledge itself, to the knower, the knowing subject.

30. There is one more way to explain this:

Every act of knowledge is perfect. And, from this point of view, every knowable object is perfect as well. This could not be in any other way: if the object was not perfect, then it would not be knowable, for it is entirely unclear how one could cognise something that is not in any way congenial to the one cognising; how knowledge could perceive something that is incompatible with knowledge. The knowledge of something that is not knowledge itself, that is, the perfect beginning, would be the transformation of an O as part of an act of reasoning into an 'not-a'. Therefore, the act of knowing does not create the perfect nature of what is being cognised, but is only explored, revealed, identified.

31. However, on the other hand, every process of cognition is real, for it is an objective, perceptible process occurring in reality. To illustrate this, albeit imprecisely, we can say that cognition manifests as a nervous process, through the innervation of vocal cords, muscular contractions and so on. Indeed, all of this is part of reality. I was initially referring to the most basic form of cognition, which can also be viewed as a material process in a subtle sense, involving various internal events accompanying cognitive acts.

Previously, we said that every thought, and indeed the objects of thought, are ideal. We will now affirm that both thoughts and the objects they represent are real. Not only is the thing thoughtlike, but the thought is thinglike as well. Thoughts contain tangible things as their content, and therefore thoughts are the creative force in the sphere of 'things'. Consider examples such as hypnosis, conspiracies, artistic creativity that transforms reality and scientific innovation that invades the real of objectivity. Thought can move a mountain into the sea; if not directly (even though indeed, directly), then implicitly, through means such as dynamite. Ultimately, the force of thought is applied to the mountain, the mountain itself, not the ghost or the idea of the mountain in the sense of pure illusion. Otherwise, man would merely be a passive observer of the fluctuations of his psyche, rather than an active participant in life and builder of culture.

32. A thought is a thought of things, and it is therefore not thinglike; it is distinct from its contents. However, at the same time, a thought is a thought of things, things are the contents of a thought, and therefore they are given to us together with the thought. I reiterate, the thought and the things form an indelible duality.

33. But there comes this question: how do potencies differ if each one of them is a duality? And what is a thing in the most common, day-to-day usage of the word?

In moving towards $A^{-\omega }$, we are increasing the ideal moment of a potency and correspondingly decreasing the real moment. Potencies become less and less thinglike, material. We are ascending ab idealia ad idealiora. On the contrary, in moving towards $A^{-\omega }$, we are increasing the real moment of a potency and correspondingly decreasing the ideal moment. Potencies become more and more thinglike, material. We are descending a realia ad realiora.

$A^0$, that is, a thing in the common sense of the word, is the balance of both moments, the ideal and the real. $A^0$ is the indifference of the subject and the object, the equivalence of I and not-I, the indifference between the knower and the knowable. $A^0$ is, at the same time, relative to the series (30), the upper bound of negative potencies and the lower bound of positive potencies. $A^0$ is the maximum of perfection, or consciousness, in the realm of the unconscious, and the maximum of reality, or unconsciousness, in the realm of the conscious. Conversely, $A^0$ is the minimum of reality in the realm of the unconscious and the minimum of perfection in the realm of the conscious.

Therefore $A^0$ is the border of the two worlds. We can refer to one of these worlds, the world of positive potencies, as the world of I in the broad sense, and the other, the world of negative potencies, as the world of not-I, also in a sense that is broader than the common. But thereby we must not forget that every potency is objective relative to some and subjective to others.

35. What, in this case, is the 'pure subject', that is, a potency such that it is a subject in relation to all other potencies but is never an object for any potency? What is the pure form or the scheme of subjectivity? What is the limit of subjectivity? In other words, what is the transcendental subject, the subject in itself? It is clear that it should be outside of the series of potencies (30), i.e. it is transcendent to knowledge, even thought it is postulated by knowledge, that is, the series (30). It is the perfect right bound for the series (30), the upper bound of the series (30) and, in relation to knowledge itself, as part of knowledge, gnoseologically, cannot mean anything other than pointing out the possibility for knowledge to be ascending infinitely, ab idealia ad idealiora. The gnoseologically transcendental subject, the pure I, is none other than the entire series (30) in its ideal aspect. What is the pure I? It is everything but taken in its ranked relation to perfection; the ordered everything, for it is ideal. The gnoseologically transcendental subject is never given to be cognised (for in that case it would be an object), but is only ever supposed. To summarise, it is what we denoted with the symbol $A^{\omega }$.

36. We must also ask what a pure object is; that is, a potency such that it is an object in relation to all else but is never a subject. There is more: what is the pure form or the scheme of objectivity, the maximum thinghood or the limit of objectivity, thinghoodness? In other words, what is the transcendent object, an object in itself or a thing in itself, or rather about itself? It is clear that this object must be outside of the series of potencies (30), that is, it is transcendent to knowledge, even though it is postulated by knowledge, that is, the series (30). This is the perfect leftmost boundary for the series (30), the lowest boundary for series (30), and, in relation to knowledge itself, as part of knowledge, epistemologically, it cannot mean anything other than pointing at the possibility for consciousness to descend ad infinitum, a realia ad realiora. The gnoseologically transcendent object, a thing in itself, a pure not-I, is none other than the entire series (30) in its real aspect.

What is the pure not-I? It is everything considered in a ranking in the context of reality, ordered by how real it is. The gnoseologically transcendent object is never given (for it would then be a subject!), but only ever considered. To summarise, that is what we would denote as $A^{-\omega }$, for if we were given $A^{-\omega }$, then we could form $A^{-\omega -1}$, and $A^{-\omega }$ would become a subject.

37. There is more. The transcendental subject is all knowledge (the cognising) as a whole. The transcendent object is all knowledge (the knowable) as a whole. In reality, they are the same; yet they are different by type if we use Cantor's terminology. In reality, the absolute I is the same as the absolute not-I, and both are equal to any final potency. Everything is in everything, and therefore everything is equal to everything.

38. All of the above can be illustrated with the following scheme:

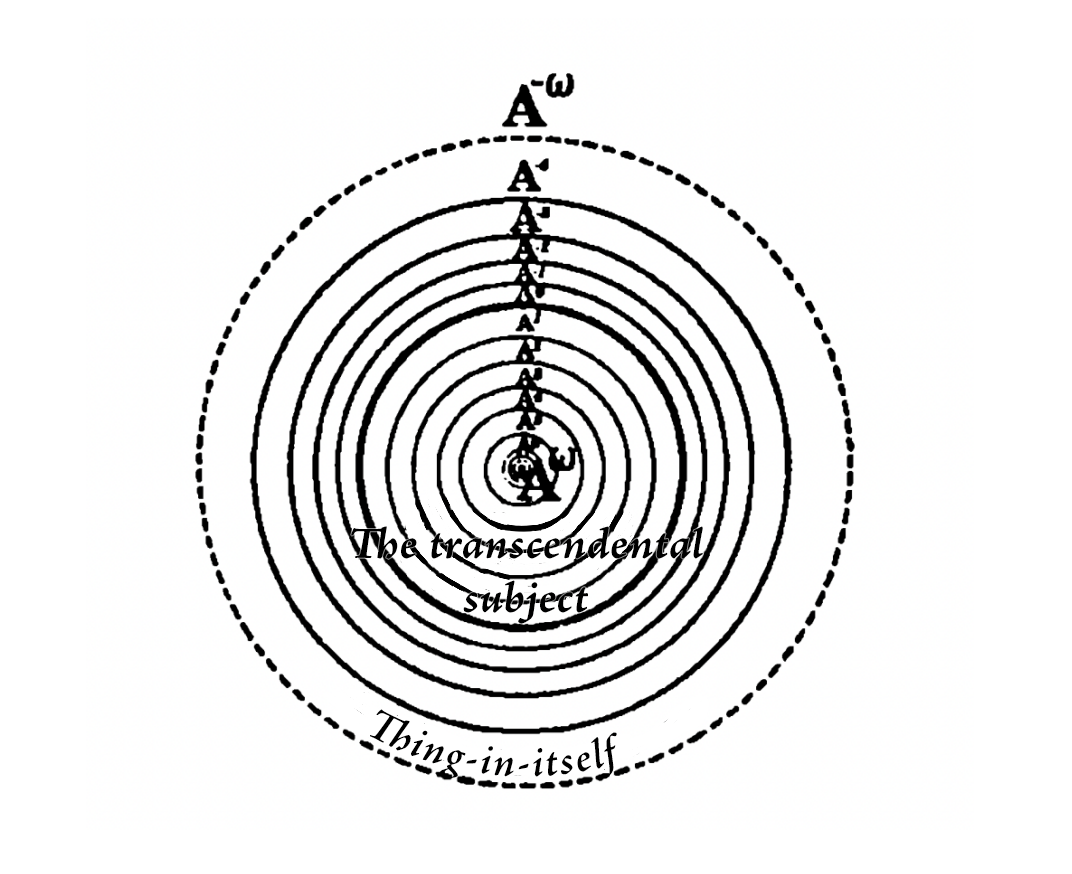
Let us draw a system, i.e., an infinite set, of concentric circles that, on the one hand, gravitate and accumulate around the centre, that is, infinitely approaching the centre that denotes the transcendental subject $A^{\omega }$. On the other hand, these circles infinitely increase their radius and aim for the infinitely-large circle that denotes the thing in itself, $A^{-\omega }$. One of the circles, $A^0$, serves he bound of I and not-I, or a thing. All other circles are denoted as $A^i (i=\pm 1, 2, 3, ..., n, ...)$, ordered according to the series (30). Let us then colour all these rings; for example, the outer rings shall be blue and the inner rings shall be pink. The depth of the colour of the area between the pairs of concentric circles will denote the relation to either the subjective or the objective side of the series (30), and the colour itself (red or blue) the dominance of either subjectivity or objectivity. The circles within the circle $A^0$ denote the realm of I, and the circles outside of $A^0$ denote the realm of not-I.

39. It would perhaps be appropriate to draw the circles that denote negative potencies as approaching the extremum circle of the final radius, which, again, denotes $A^{-\omega }$.

40. Let us continue examining the system of potencies of knowledge (30). The Nth act of knowing, $A^n$, is knowledge of the object $A^{n-1}$. But $A^{n-1}$ is knowledge of knowledge, $A^{n-2}$. $A^{n-2}$ is knowledge of knowledge $A^{n-3}$, and so on, up until $A^0$ inclusive. And from there on: $A^0$ is knowledge of $A^{-1}$, $A^{-1}$ is knowledge of $A^{-2}$ and and so on. Therefore the contents of $A^n$ include not only $A^{-1}$ but also $A^{-2}$, $A^{-3}$, $A^{-4}$ and so on; also $A^0$, $A^{-1}$, $A^{-1}$ and so on. Therefore every act of knowing $A^n$ includes the entire infinity of contents, the entire series (30) up until $A^{-n-1}$ inclusive, that is, the entire field of the subconscious, all the preceding An degrees of knowledge. The contents of $A^n$ are every $A^i$ where $i<n$.

41. Yet there is more. We have the act $A^{-1}$, which, as we have already seen, is the act of destroying an utterance, the act of confusion, obliteration, transfusion, obfuscation, etc., that is, it is the opposite of $A$. If we have this act, we can examine the relation of $A^n$ to all potencies that follow it. By applying the operation $A^{-1}$ to $A^{n+1}$, $A^{n+2}$, $A^{n+3}$ a certain number of times, we will keep getting the same $A^n$.

$A^n=A^{-1}\left(A^{n+1}\right)=A^{-2}\left(A^{n+2}\right)=A^{-3}\left(A^{n+3}\right)=... \left(31\right)$

And generally: $A^n=A^{-m}\left(A^{n+m}\right) \left(32\right)$

Therefore $A^n$ includes in its contents not only the entire series of lower potencies of knowledge, but the entire series of larger potencies also.

42. Yet it is only $A^{n-1}$ that is the immediately knowable potency for $A^n$ All other potencies that precede $A^{n-1}$ (i.e. all $A^i$ for which $i<n-1$), in relation to $A^n$ ('the empowered knowledge') are below reason and below knowledge.

On the contrary, all potencies that follow $A^{n-1}$ (i.e. all $A^i$ for which $i>n$), are beyond reason, above knowledge. Some are already not cognised, and some are not cognised yet. One is the infinity before, and the other is the infinity after. One is the oblivion of the past, and the other is the neglect of the future.

43. Indeed, the validity of this new approach to knowledge, of shining the light of the idea of time on it, is evident from the following.

The continuity of potencies of knowledge creates the idea of time. Moving towards the positive side of the series of the transition from the past towards the future. Moving in the opposite direction is the transition from the future towards the past. As such, the conscience of the dying, of the drowning, of those falling from mountains, etc., when the organism is deprived of knowledge (loss of memory, weakness, etc.), creates the reverse time series, from the present towards the past. And vice versa, the creative act of knowing brings us towards the future, gives us the gift of foreboding. Confusion is losing oneself in the present, an act of moving into the past; and, respectively, creativity is the act of moving into the future. Both losing oneself in the present, i.e. confusion, and creativity draw one out of the present, but in two opposite directions.

And so, if $A$ is the present (in the present), then what is the past? It is the system of potencies $\left\{A^i\right\}$, for which $i<n$. What is the future? It is the system of potencies $\left\{A^i\right\}$, for which $i>n$. The subject of knowledge is the future; the object is the past; the act of knowing itself is the present. The thing in itself is the absolute past; the transcendental subject is the absolute future.

44. We shall now focus on how the series of potencies begets the series of time. Indeed, if our series of potencies (the law of the expansion of consciousness) must be the source of the historical process of philosophy, then this series must, as we said, be historiogenic by nature. But, as it creates history, it cannot be historical itself, it cannot itself be history in the strict sense. It is historiogenic and therefore not historical itself. It is outside history and therefore outside time. Therefore, it must contain forces that unfold its contents; as a process in time or forces that beget time that is full of historical events; chronological forces, time-begetting forces. Apparently, this is where the stumbling block lies. Perhaps you have already thought: but to go from one potency to another, you already need time. How could it be that the series of potencies produces time when it needs time to be formulated? We have arrived at an idem per idem in our reasoning. Time is the condition of the series, and the series is the condition of time. We have numbered the elements of the series. But is the act of numbering itself not a sufficient proof that a series cannot be without time, for numbering, the order of sequence, by itself presupposes time and cannot exist without time? I will answer your questions with a question.

Is it true that every ordered list or sequence presupposes the concept of time? Or is it perhaps possible for a logical sequence to exist without time or maybe even outside, above time? I will now very briefly answer this question.

Consider some kind of complex system of reasoning. It could be a philosophical system or any other, preferably a strictly logical one. For example, it could be Spinoza's system the way it is outlined in his Ethics, or some sort of geometric theorem. If you are reading it or reflecting upon it for the first time, its distinct aspects and arguments may seem, formally and externally, awkwardly glued together. The reasoning mechanism is clumsily moving forward. Upon a second reading, you will notice that this movement is much easier and smoother; the system's distinct aspects begin to interconnect more closely and grow into one another. With a third reading, the movement is even faster, and the parts integrate even more organically. You will eventually come to perceive the entire line of reasoning as a unified whole, as an organic body composed of organs. We distinguish between the first moment, the second moment, etc., but we cannot say that these are moments of time. No, these are logical moments, dialectic moments, aesthetic moments, moral moments, etc. The entire reasoning process approaches the limit, the zero of time, striving to become momentary. From here, we postulate the momentary sequence, this limit, as reality. I will later try to demonstrate that this reality does in fact exist. For now, I will only say that what is actually important to us is not the reality itself but the very concept of it, the concept of a sequence of moments existing outside of time. We will now use this concept of a timeless, atemporal sequence to prove the origin of the idea of time from the atemporal series of potencies.

45. It might not seem entirely clear how this system of potencies is the future or the past. Yet that is, of course, true. Because what is the past or the future if not $A^n$, a part of the contents of the present conceptualised in this present already in a certain way? The coordination of supposed, relative parts of the present is the characteristic by which we refer to one part as the future, the other the present in a narrow sense and the third part the past. Yet what is coordination if not a ranking of parts relative to each other (that is, ordering parts in a way where one begets the other, the other begets the second, the second begets the third, etc.)? Numeration; that is what forms the idea of time. The heterogeneous quality of potencies is what gives space to numeration; quantitative differences are merely projections of qualitative differences on the temporal series that the latter beget. Quantitative differences are superstructures of qualitative differences. To summarise, it is now clear how the idea of time corresponds to the series of potencies:

$A^{-\omega } ... A^{-2}{A}^{-1}{A}^0{A}^1{A}^2{A}^3 ... A^{n-1}$	$A^n$	$A^{n+1}{A}^{n+2}{A}^{n+3} ... A^{n+m}...A^{\omega }$
the past	the present	the future

46. Yet why is the present only a point in time? Why by the time we are discussing it, it is already gone? Why can we only talk about the past? Why tempus fiigit? Why is it irreparabile?

The present is a point in time because it is a singular potency, that is, a singular act that does not have distinct parts. Therefore an act that differentiates is not a manifold act, it is completely simple. When we speak of the present, there is no present, for when in order to speak of the present, of $A^n$, we need to make it our object (previously a subject). Once it is the object, it is now lower in rank than the subject of speech, $A^{n+1}$. That is precisely why we can only speak of the past, i.e. one of the past potencies of knowledge. Does tempus fugit? No, for we do not think and do not live. The passage of time is an illusion of the same kind as the round dance of the trees you see when passing them on a train. It is not time that moves away from us, but it is we moving away from the present, from $A^n$ towards $A^{n+1}$, $A^{n+2}$ and so on. We do that by means of cognising that $A$. If we were not cognising it, if there was no ongoing reflection (a frozen consciousness; loss of consciousness; narcosis; dreaming; etc.), then time would not be moving away from us as well, and we would be stuck in an eternal now. You will say: but to others, objectively, this person would still exist within the context of time?

Yes, to others. That is, they would be changing their present relative to that person. If they were not changing their present relative to him, he also would not live in the context of time for them: 'as the call, so the echo'. When someone wakes up after a long sleep, narcosis or coma, he is akin to a fairy tale princess who does not know whether time has passed. He did not live in the context of time.

47. We repeat here the Copernican Revolution, but on a much larger scale. Just as Copernicus described the movement of celestial bodies, we now apply that concept to all forms of movement and change, including time itself, which we understand as the perfect and pure form of movement. Copernicus asserted that the Sun's movement is only seemingly real and is conditional upon our own movement. Similarly, we propose that time does not actually pass; it merely seems to pass because we change our perspective on our acts of cognition, acts of knowledge. We are passing a series of potencies, and it appears to us that the series of potencies is passing us. This passing of potencies in our knowledge is what we refer to as time.

48. Yet let us return to our potencies. Every act of knowing $A^n$ includes all the infinite acts of knowing from its past and its future. We are using the terms the past and the future in the sense of a qualification of time. In other words, every act of knowing includes a forgotten thing in itself and the forgotten transcendental subject. Even though the thing in itself is transcendent to knowledge and the pure subject is transcendental, they are still contained within every act of knowing.

49. We think what we are already not thinking, and we think what we have not yet thought. We know what we do not know already and what we have not yet come to know. Yet everything, the past and the future alike, is in some sense contained in us, for potential knowledge is not an abstract ability to cognise, not the absence of knowledge, not οὐκ ὄν‚ but the true power of knowledge, a special state of knowledge, μὴ ὄν: not the lack of knowledge, but knowledge that is present in a special way.

50. It follows that all recognition is recollection, either of a past state of knowledge, knowledge in its past form, or of knowledge in its future state. We could also include here the discrete transmission of potencies of the overconscious realm into consciousness; as a result of this transmission, they become timeless, atemporal. It would be appropriate to refer to these mystical processes as the memory of the present.

Furthermore, there exists a form of 'memory of the future', just as there is the memory of the past. Both are connected with order within time, but both bring the past and the future, with their characteristics, to the present. But are the future and this memory found in concrete psychology? The coming of the future itself demonstrates that we 'remembered' it, that we recognised it. When consciousness gets ahead of oneself, darting across the series of potencies, is when forebodings and foretellings of the future appear. These chaotic movements also include the phenomena of paramnesia, premonitions, clairvoyance and clairaudience, prophetic dreams and the anticipation of scientific ideas and discoveries. The Platonic teaching of knowledge as remembrance, recollection, άνάμνησις of Heaven, is also related to these processes. The same can be said of Nietzsche's teaching on the eternal return. Psychologically speaking, both are based on the phenomenon of paramnesia that makes us feel like we have already lived through this particular moment before. Every scientific work is contained within the previous work, and vice versa; if you take a close enough look, you will find one in another. This is the simple truth the poor understanding of which led to the historicism of the 19th century, with its exaggerated and uptight attention to all sorts of historical 'influences'. It is indisputable that within every work, one can find all prior works and those that will follow, all contained within it like folded leaves in a tree bud. Often, the author may be unaware of their connections to the past or future and may not fully understand their own work. However, a scholar of someone else's thought will inevitably notice its many links to that of others. We have to recall here the words of Heinrich Hertz: sometimes mathematical formulas appear more clever than their creators, as they encompass ideas that the composer might never have consciously considered and that are only discovered later. This magical power of formulas stems from the composer possessing knowledge he may not realise he has. Again, we recall here the words of Heinrich Heine: 'When a writer is creating their work, he feels, according to Pythagoras's teaching on the transmigration of the soul, as if he has lived many lives, wandering the world in various forms. His inspiration embodies all qualities of remembrance.' Finally, we should also acknowledge the remarkable ability of great writers to predict their own fate within the symbolism of their works, as seen in Lermontov, Pushkin, Gogol, Byron, Oscar Wilde and others.

51. We can summarise all the different kinds of memory as follows:

Memory of the past	Paramnesia
	Hallucinations about the past
	Dreams about the past
Memory of the present	Clairvoyance and clairaudience (without clear images)
	Hallucinations (with clear images)
Memory of the future	Premonitions (without images)
	Prophetic dreams
	Creative expression and art
	Hallucinations about the future
	Anticipation of scientific ideas

52. In addition to orderly knowledge, which involves sequential transitions from one potentiality to another, there exists a separate vast realm of knowledge that can be described as chaotic and disorderly. This broader category of knowledge can be referred to as mysticism, or, to be more precise, natural mysticism, to differentiate it from supernatural or graceful mysticism.

Mysticism is what gives us the knowledge that reveals the existence of multiple layers of reality and various negative potencies. First of all, this is about manifold dreams. Many of us have experienced dreams within dreams, where we seem to wake up only to find that we are still in a dream state. It would turn out the first time we woke up was inside a dream. This is known as a twofold dream. There can also be threefold dreams, fourfold dreams, and so on, in which the dreams continue in layers (n-fold dreams).

Yet have you ever noticed that transitioning from a deeper layer of a dream to a regular dream is accompanied by a sense of heightened awareness? This shift from a profoundly unconscious state to a comparatively conscious one often feels overwhelming and heavy, leaving you in cold sweat. It is akin to the sensation of a sudden fall or being pulled into a whirlpool. Conversely, returning to simpler dreams or waking up feels like an ascent; like swimming upward, jumping out or being carried along by a current. In this stunned state, the dreamer often forgets the dream entirely. It is quite likely that the Platonic teaching of forgetting Heaven, where the soul, upon descending into the material world, is overwhelmed by matter, should be understood as the mythologising and ontologising of those or similar experiences. I will not go into too much detail descriptions of these n-fold dreams and correspondingly n-fold awakenings. We find such accounts in fine literature: in Shelly, Wagner, Hoffman, Gogol, Lermontov and others.

Hypnosis provides an even clearer image of those transitions of I from one layer of subconsciousness into another. Many individuals who have experienced hypnosis know that immersion into one or another degree of subconsciousness very well, especially when it occurs suddenly or quickly. Such abrupt shifts can be alarming for the person being hypnotised, prompting him to exert all effort to wake up. That either disrupts the hypnotic state or, in any case, does not let it proceed as intended.

The thing that barbaric initiations into mysteries of secret religious societies refer to as a 'temporary death', which all initiations everywhere would require the novice to experience, is, again, one of the rather significant degrees of subconsciousness, the negative potency $A^{-n}$ with comparatively significant $n$. The different 'plans' of theosophy, quite likely, are also related to the negative degrees of knowledge.

53. To conclude, all knowledge is remembrance, recollection, as Plato taught. Knowing, άνύμνησις, an act of recollection of what the soul saw before it was born. That is what Plato said. Yet this mythical formulation of the gnoseological truth is a projection of gnoseological knowledge on a series of time, whereas in reality the series of time and therefore myth is born of the ranking relations of gnoseological elements. All science in nuce is contained in every one of its given states. All acts of knowing are in this singular act. Every statement is all philosophy. Knowledge, no matter how limited it might be, is infinite by its very nature and is therefore irrational. No matter how clear knowledge might seem, it is clear only under the shining cloak of 'the present' ($A^n$) but murky in both its aspirations, towards both $A^{\omega }$ and $A^{-\omega }$. Every one of our thoughts touches on the infinity of knowledge. Every act of knowing stirs all of knowledge in the soul.

54. That is the only way to explain why it is possible to be satisfied with limited, finite knowledge. Finite is infinite; a part is the whole; one is everything, εν και παν, the conditional is unconditional, the temporary is eternal. To understand that in this finite potency of knowledge that corresponds to the epoch and moment of history and our personal lives contains infinite contents, and we should therefore restrain our lust to fully know and cognise these contents and stop reaching for the future at all times; that is what it means to live in the present. This also brings wisdom, for such a person does not judge all eternity by the present day but sees through the present day and discerns in it all eternity.

55. And as such, the rationalistic epistemology starts with the subjective moment of knowledge and covers all the different kinds of knowledge, explaining all the major concepts in epistemology in its own way. Yet its coherence, on its own, does not yet tilt the scales in favour of rationalism, for we do not at all have any grounds to assert that realism (or its purest form, intuitivism) will not find its own answers to the same questions about knowledge.

Footnotes

1. This article was originally written as part of the course Introduction to the history of Ancient philosophy, which Fr. Pavel Florensky taught at the Moscow Theological Seminary in 1908 and 1909.
2. The line of reasoning presented in these few paragraphs was originally inspired by Schelling, duke Trubetskoy and Michael Ostroumov (specifically his History in relation to the Revelation, Kharkov, 1886).
3. Ostroumov, p. 18.
4. We could, with less formality, reason as follows:

$A=A\left(1\right) \left(I\right)$

that is:

• Either multiplication, for $\mathrm{A}=\mathrm{A}*1\mathrm{;}$
• Either potentiation, for $\mathrm{A}={\mathrm{A}}^1$
• But not a sum, for $\mathrm{A}\ne \mathrm{A}+1$
$\left(14\right)$

The first formula demonstrates that operation A is either multiplication or potentiation. Then, trying our luck with using the symbol $*$ for any kind of comparison between two potencies, we have:

$A_n*A_{n-1}=A_{n-1}*A_{n-2}=...=A_2*A_1-A_1*A_0 \left(15\right).$

$*$ can stand for either substraction or division.

Translator's notes

a. In the original Russian, all these words share the same root, ultimately being formed from knowledge (znanie). Cognition is poznanie, consciousness is soznanie, self-reflection is samosoznanie and self«самосознание», «самопознание».

---

Translated from the version published in the Theological Bulletin, Volume 1, Issue 1, January 1913, Pages 147-174: